Pitches

Pitched roofs

 

Any carpenter knows that the basis for roof framing is math. It is almost impossible to frame a roof without knowing any mathematics, especially trigonometry. It is needed, for example, to calculate the steepness of a roof - the roof pitch. 

In Nordic climate, a pitched roof is preferred so that rain water would not be accumulated on the roof, which would happen in case of blocked water drainage with a flat roof. One of the main reasons for blocked drainages is the cold weather which causes blockages when the water turns into ice; other reasons include leaves, debris etc. 

For this reason, throughout time, pitched roofs have been preferred in Nordic countries. 

Pictured below is an example of a flat roof and a pitched roof:

As we can see, the simplest and most common pitched roof is shaped as a single triangle. The situation becomes more complicated when two or more pitched roofs are joined together. This creates a number of different slopes in one spot which need to be attuned together (constructed).

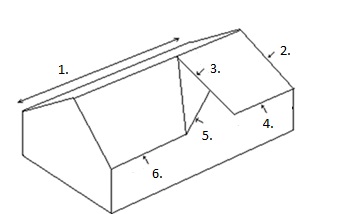
1.       Ridge 2.       Hip 3.       Gable 4.       Eave 5.       Rake edge 6.       Eave

Source: OÜ Plekk – Katusemeister

Here we can see the different angles and shapes than can occur on a roof.  

 

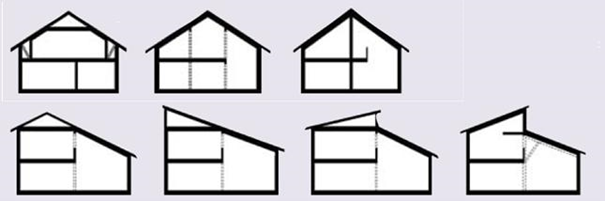
Pitched roofs can be in many different shapes, most common ones are gable and hipped roofs. There are also roofs that are not so simply shaped. Below are pictured some different shaped pitched roofs:

 

 

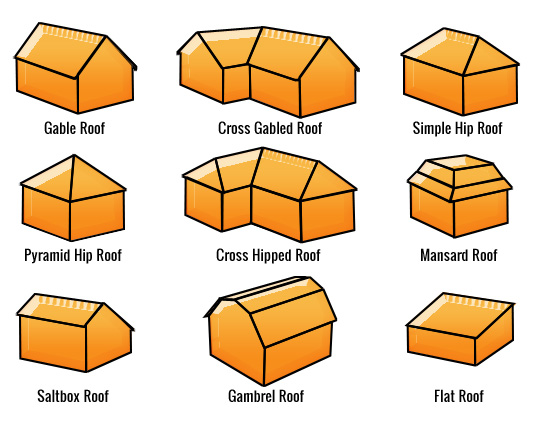
Source: Shelton Roofing Santa Cruz

 

Source: Insenerigraafika. Olga Ovtšarenko (e-õppematerjal)

 

Pitches 

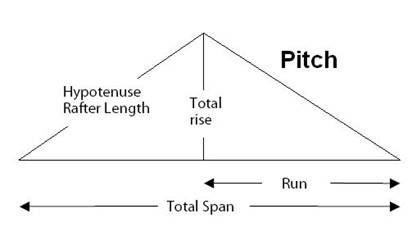
Carpenters do not refer to the angle of roof as 30° but prefer to use the pitch of the roof. The roof's pitch is its vertical rise divided by its horizontal span (or "run") -called slope in geometry or the tangent function in trigonometry.

On the figure below, the various permitted pitches for different roof materials are depicted. For example, in the case of rolled metal roofs it can be a minimal of 5° (as shown on the graph). This means we cannot use rolled metal for flat roofs because it would not be a waterproof construction.

1: lath and shingle

2: ceramic roof tile

3: skylight

4: bitumen roll with triangular lath

5: asphalt shingles

6: cement roof tile

7: bitumen wave plate and tin roof sheets

8: fibre cement board

9. rolled metal roof

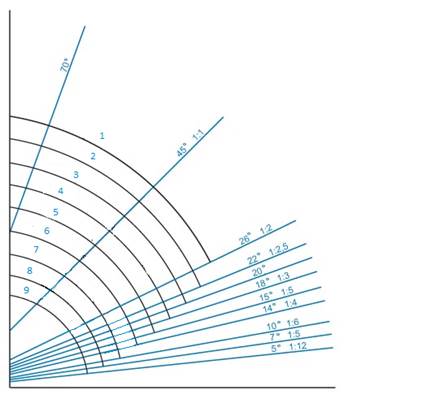
In the above graph we can also see the different values given as a ratio - for a slope of 5° the ratio is 1:12. We know that on traffic signs the slope of a road is also given but it is shown in percentages. 

Let’s have a look how these different values are related to each other:

As we all know, a full circle equals 360 degrees. In the graph below, we can see that in case of a roof pitch, trigonometrically seen, one side of a roof is in the I quarter and the opposite side in the II quarter.

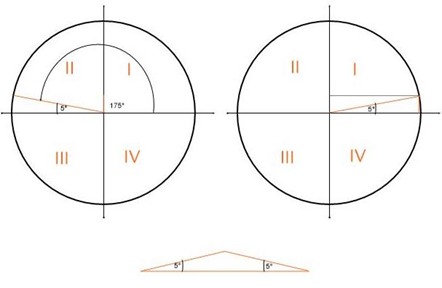
The partition of quarters can be seen in the image below: 

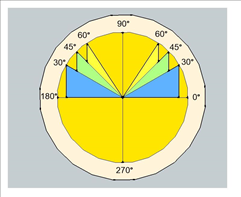
If we are talking about expressing the pitch as a ratio, it will be the ratio of the length of the segments to each other.

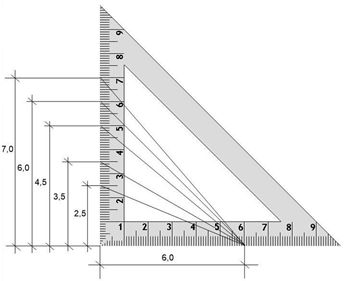
For example: if the ratio of the roof pitch is 1:1, we are talking about an isosceles triangle and the roof pitch can be given as  45°. To calculate the pitch we use the tangent function, meaning 1:1=1, where tan 45°=1

 

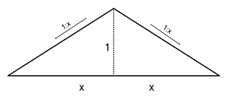
To express the roof pitch as a ratio, the height or so called rise will be given as a value of 1. The distance from the rise of the roof to the edge is marked with x (also called the run). The value of x shows how many heights till the edge the roof.

 

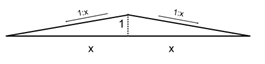
For example: if x=2, then 1:2=0,5. In conclusion tan 0,5 = 26,57°≈ 27°

 

If the angle of the roof is more than 45° or in other words the ratio is bigger than tan > 1, the run will be a constant with the value of 1.

 

For example: Given a pitch of 1,5 : 1. This means  x = 1,5 and shows how many runs fit into the rise.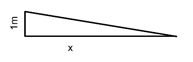

 

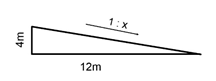
Different ways to calculate the pitch of a roof 

Problem: Given a roof with the rise of 4m and a run equalling 12m. Calculate the pitch of the roof and give it as a ratio!

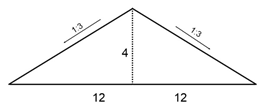
Here are 2 ways to solve the problem: 

Method 1: If the pitch is given as a ratio 1:x, we can do the following to find x: 

The pitch of the roof is 1:3 

Method 2: We can also use the following solution 

A 4 meter rise equals 12 m of horizontal length. Knowing that, we can do the following calculations for a rise of 1m :

The pitch of the roof is 1:3 

Pitches can also be shown as percentages and per mille. Percentages are mostly used for roads and hills, per mills are used for floor slopes and emplacement of water and sewages pipes, where the pitches are a lot smaller.

 

A pitch given in percentages equals 1/100  

  

1 m = 100 cm 

hence 1% is 1cm per meter 

  

1 m = 1000 mm 

 
 

therefor 1‰ is 1mm per meter 

 

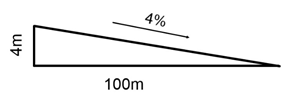
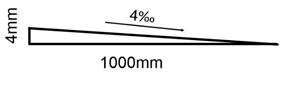
Given the values for run and rise, we can calculate the percentage or per mills of a pitch in the following way:

 

 

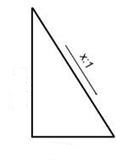
If we need to calculate one of those values, we can convert the formula. 

For example: to find the rise, we can convert the formula in the following way: 

 

 

If our run has a length of 1m (100cm), then with a pitch of 1% our rise will be 1 cm. A run with a length of 2m will have a rise of 2 cm given the same pitch.

When calculating in per mills, a run of 1m with a pitch of 1 will have a rise of 1 mm. A run with a length of 2m will have a rise of 2 mm given the same pitch.

 

To find the values for the run, we must again convert the formula: 

 

 

 

 

Sometimes we might need to build a roof with the same pitch but different measurements 

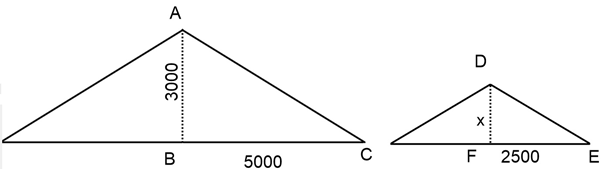
In that case, we use the principal of similar triangles to make the calculation. 

 

The calculation can be done using cross multiplication: 

When we compare the pitches, they will be the same even with a different rise of the roof.

In reality it would look like the picture below:

Let’s bring some more examples on how pitches are related to each other. For example, if we know the % of a pitch but want to express it as an angle using a tangent, we can do it in the following way: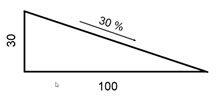

As show on the graph, given the rise and run, we will know the pitch percentage (up to 45°) and can calculate the tangent using the same ratio - it will give us the angle.

From that we can derive the angle α = 16,66924423° ≈ 16° 42’ 

 

Further explained, to get this solution we equal the run to be 100 and choose a rise that when divided by 100 would give us the %-value. Since percentage is basically the relation between run and rise, the percentage value is at the same time the tangent of the angle.

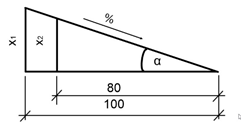
The above figure shows the given different proportions the  pitch can be the same. If however we take the run to be 1, we can show the pitch as follows:

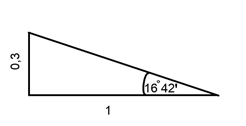
We know already that tan 16° 42’ ≈ 0,3

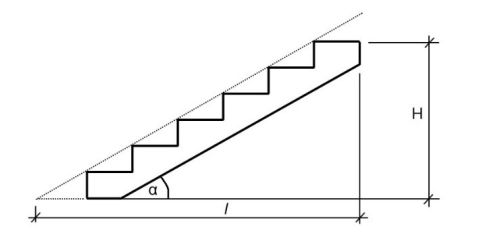
Stairs and sewers

Another part of construction that uses pitch (or slope) calculation are stairs and sewers (especially gravity flow pipes, not so much pressure pipes).

Stairs must have certain measurements so that people can comfortably use them. To calculate the height of the stairs a simple formula is used. Who wants to become a construction worker should definitely remember this formula: 

2h+b=630 mm 

This formula helps to find the optimal ratio between the rise and tread of the step.  

h= rise of the step  

b= tread of the step

   

 
 

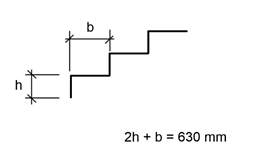
The sum of double rise and the tread gives a constant. From that the pitch can be derived - usually 1:1,5 to 1:2.

For the width of the steps the formula h + b = 450mm is recommended.

Additionally to the pitch, the stairs will have a total rise and total run which are also important measurements.

 

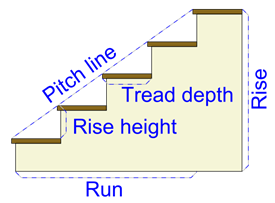
Image: Wikipedia 

 

 

When building  multi-turn stairs you must also make sure that it has an uneven number of steps otherwise you must change legs when walking up the stairs. All steps must also have the same rise - human brain adapts to a certain rhythm of walking so if one step is of different height  than it might cause you to trip on the steps. 

 

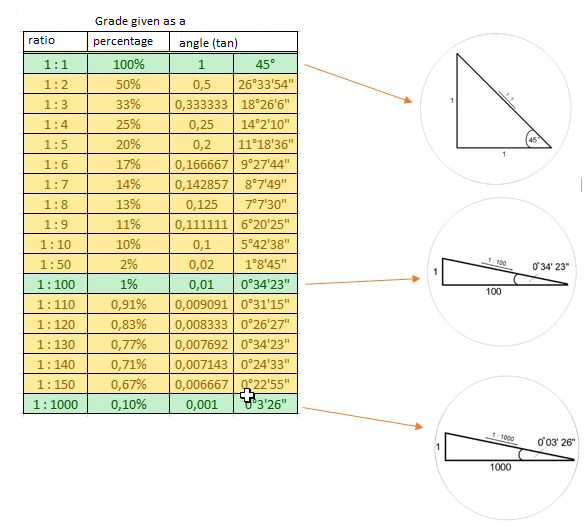
The above table shows that given the ratio 1:1 the triangle will have the exact shape as pictured beside  - an isosceles triangle with 45° equalling an angle of 100% and a tangent of 1. 

Given the ratio 1:100, the grade will be as pictured on the side with an angle of 1% and tangent 0,01. With 1:1000 the same logic applies.  

 

For example 

If we know the value of the tangent then we can write the pitch as a ratio in the following way: 

Given tan 0,5 = 26° 33’ 54,18’’ 

Mark the pitch as a ratio 1 : x where x equals 0,5 (also the tangent) 

Hence the pitch can be given as 1:2 
 

 

The value of x in the ratio represents  how many parts of the whole it composes since 1 represents the whole (l=1 on the graph) , so 1 : 0,5 = 2.  You can also show the pitch as a measurement of a whole.

 

As already mentioned, if the rise (h) is greater than the run ( tan > 1 ) , then the value of x is above the value of the part pitch is  denoted: x:1

For example, if the value of the tangent is 2 value of the slope is 2 : 1 

 

 

In sewage pipes we also use pitches but there it is given in per mille. 

Pictured below is a  cross section of  a sewage line, which is used for pipe grades in construction drawings. As you can see the distance between the two wells (from the centre) is 34500 mm and the difference between the heights of the wells is 300 mm. 
 

 

Let’s look at another example. How to calculate the pitch of a pipe as a ratio and in percentages. In order to calculate the pitch we must sketch a triangle where h marks the difference in height and l the distance between two wells.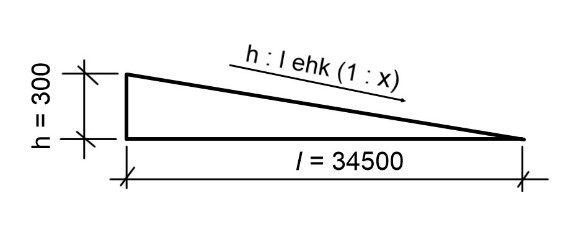
 

 

Given h=300mm and I=34500. Using cross-multiplication we can first calculate the pitch as a ratio. 

 

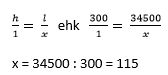
Substituting x with the value we get the pitch 1:115

 

We can also use cross-multiplication when we know the pitch  (1 : 115) and want to calculate the difference between the heights h.

 

 

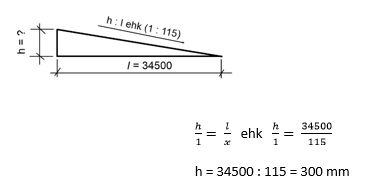
The same goes for l. 

The pitch given in percentages is: 1:115 x 100 ≈ 0,87%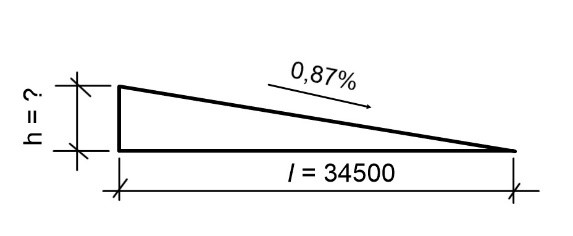
                                

On the other hand, if we know the percentage we can calculate the ratio as follows: 

 

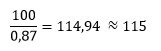
this can be given as a ratio 1:115

 

In order to calculate the pitch in percentages we must use the tangent

option 1: tan = h/l    

option 2: ratio 1 : x

tan = 300 : 34500 ≈ 0,0087 or as a ratio which is basically the same 1 : 115 ≈ 0,0087

tan 0,0087= 0,41011655° or 0°24’36,42”

 

In the picture below a sewage line in depicted in the ground before it has been covered with soil.
 
 

 

Area calculation

A big part of construction is calculating volumes. It is necessary for planning and ordering materials and for price quote calculations.

 

 

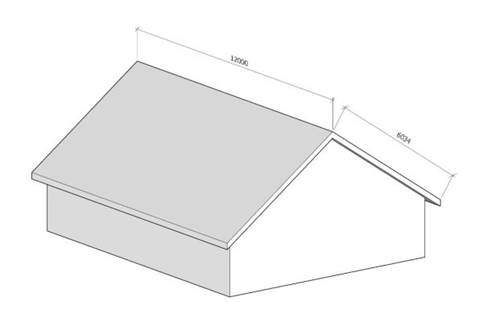
For example, sometimes only the pitch and the height from the ground are shown on a project drawing. In order to calculate the area of the roof we must know the length and width of the roof (on the picture above: 12 000 mm and 6034 mm) But if we only know the pitch we must take the drawing and based on the width of the building calculate the measurements of the roof. 
 
 

 

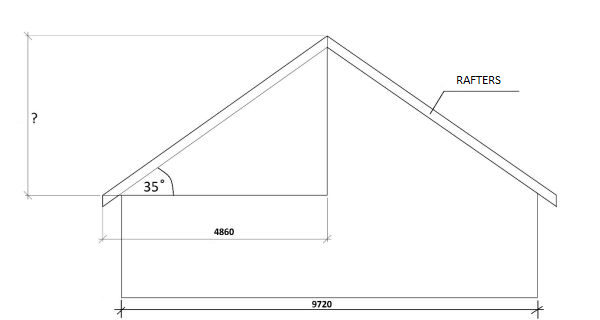
These measurements are not only needed for calculating the quantity of needed  materials  but also for constructing the roof, for example the length of a rafter.

 

For example

Given the width of half the building is 4860mm, then with a pitch of 35° the height of the roof will be:

tan 35° x 4860 mm = 3403 mm

Knowing the height we can calculate the length of the rafter.

In order to calculate the angle between the rafters we can use basic math. All we need to know is what angels occur when we cross two parallel lines with a third line. 
 
 

 

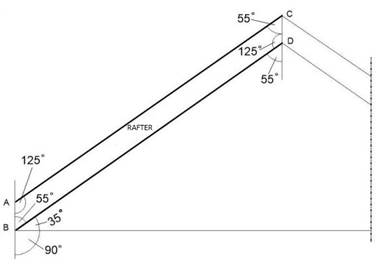
When dealing with complicated surfaces we must divide the area into parts.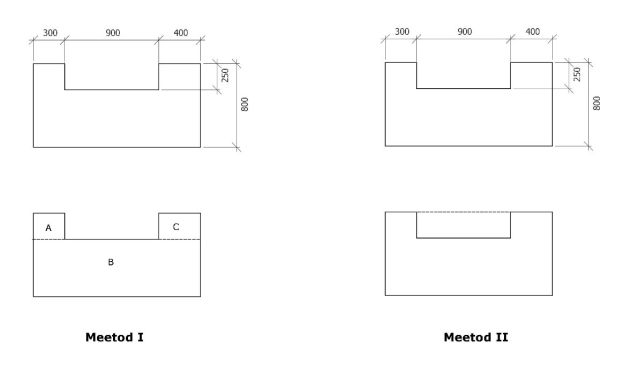

 

As we can see on the graph above there are different ways to make the area measurements easier. One way is to divide the area into many smaller areas and calculate their areas separately and then either sum up or subtract the individual areas.

 

But how do act if the roof has more than one angle like shown below: 

 

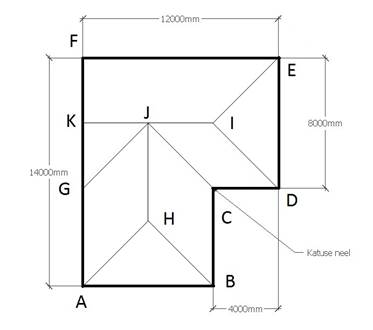
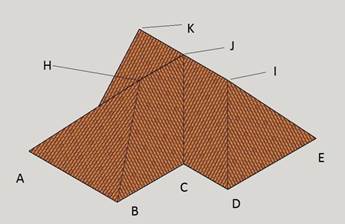
This is a 2D drawing of a roof which is given in the project drawing, next to it a 3D drawing is usually also given.

The pitches on the drawing are given on a 45° angle. The hips at the ends are also at 45°. If we draw a notional line vertically from H,I to K, their pitch will be 45°.  If we know the angle and the length of the roof, we can calculate the height of the roof that we will need later in order to calculate the area of the roof. 

Since the angle is 45° we know that we are dealing with an isosceles triangle that has two sides of equal length. This makes our calculations easier. 

For example, the height of the roof is half the width of the roof, or 4000 mm . This can be seen in the figure below , which shows a side view of a roof. To calculate the length of the hip we will need a calculator.  

We can use the Pythagoras theorem since the length of the hip is equal to the hypotenuse of A, B and H.

The length of A,B and H equals  

 

 

 

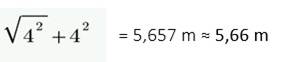
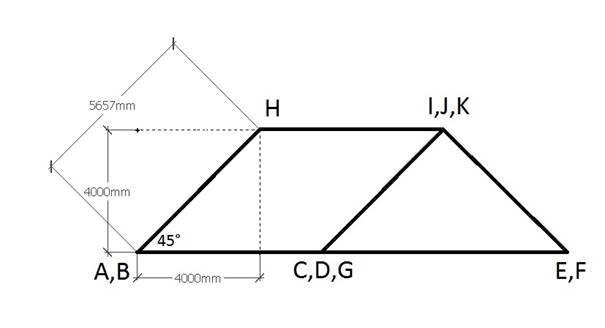
This is the height of the hip end, which from the viewpoint of the hip would look like:

 

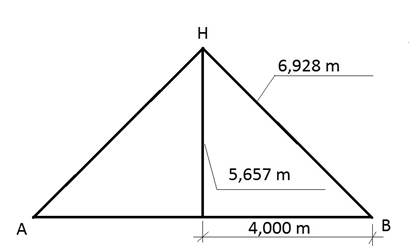
BH is the hypotenuse and represents the height of the roof. The solution was obtained by the Pythagorean theorem. The length of the hypotenuse is :

 

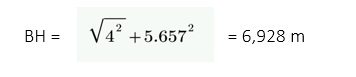
Since this is not an isosceles triangle, we can draw the conclusions that although all roof pitches are at 45 degrees, it is not the case for his hip angles .

If we know these measurements we can start calculating the area of ​​the roof . We can see that the roof elements are composed of different geometric shapes. As a reminder, let's see which formulas we will need.

 

 
 

 

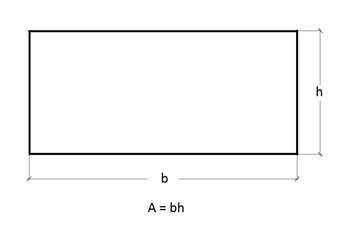
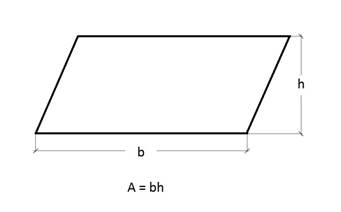
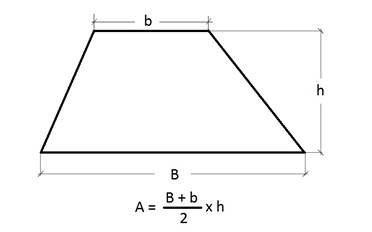
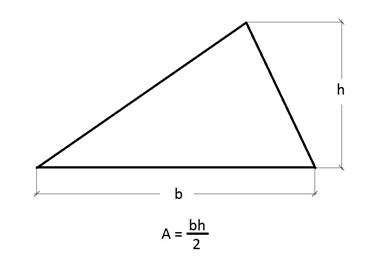
We can calculate the area as follows: 

The hip ends of the roof form equal triangles ABH and DEI.  Therefore, it is sufficient to compute the area of ​​one triangle and multiply it by 2 .

 

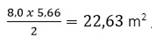
2 x 22,63m2 = 45,26m2

 

The parallelogram-shaped roof parts ( BCHJ and AGHJ ) are also equal, so we only need to calculate the area of one and multiply it by 2.

To calculate the area we must also know the value of HJ. This is equal to the base and doing a quick calculation we know it should equal 6,0 m. Since it has the same pitch and height as the hip we know the height of the parallelogram to be 5,66m

Thus, the area equals:

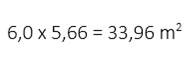
And 2 x 33,96m2 = 67,92 m2

 

DEIJ is also a parallelogram with a height of 5,66 m and a base of 4,0. Its area equals:

 

 

We can also see a triangle (KLG) – its side GK has the length 5,66m. Its other side is 4m. Based on these measurements we can calculate the area. Its hypotenuse is the side GJ which is 6,93m long.

Therefor we can calculate the area of the triangle:

 

 
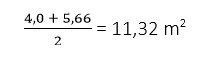
Only one part remains – the trapezoid (EIKF). We know that EF is 12,0 m and IK 8,0 m long.  We have already calculated 5,66 m to be the height.

Again we can calculate the area:

 

 

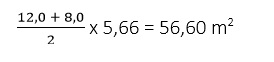
Now we can add all the areas together to get the total area:

45,26 + 67,92 + 44,64 + 11,32 + 56,60 = 225,74 m2

 

 

Overlapping surfaces

It is not uncommon that the measurements of a detail vary from what it should be when constructing all details together. For example floorboards. 

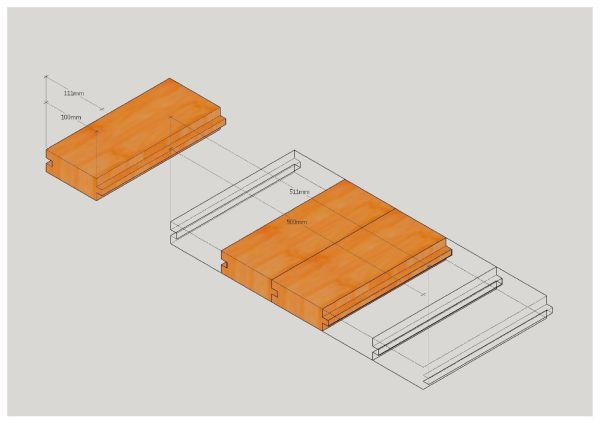
In the picture below You can see a floorboard which has a protruding part and which makes it wider then it would be when the whole area is covered with floorboards. When measuring we know that a single floorboard has the width 111 mm, but when joining it with another board it will only have the width of 100mm.
 

 

Therefore at most times timber salesmen mark the total coverage area of floorboards on the package.

 

An example 

Given a floor with measurements 6,27 m x 4,37 m. How much flooring material must we buy to cover the whole floor given floorboards with an overlap of 100 mm and a length of 4 m.

We start by calculating the area of the floor surface:

6,27 m x 4,37 m = 27,40 m2

Next we calculate the area one floorboard would cover:

4,00 m x 0,1 m = 0,40 m2

Finally we'll calculate how many floorboards we must buy to cover the whole floor:

27,40 m2 : 0,40 m2 = 68,5 ≈ 69 pieces of floorboard 

 

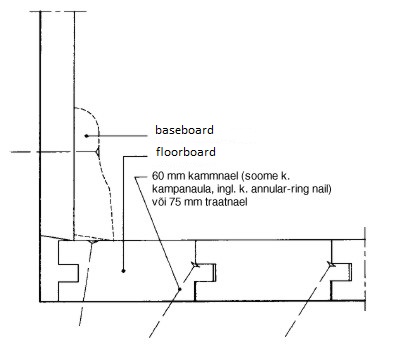
Another important part of wooden floors is the baseboard. For the floor size given above to find the amount of baseboards needed You must calculate the perimeter of the room. The purpose of the baseboard is to cover the nailheads and often it is not possible to install the last floorboard close enough to the floor and a 1-2 cm gap is left. The baseboard is used to cover the gap as shown on the picture below. 

 
 

 

An example

It is best to calculate the amount of baseboards needed by running meter because they are installed on the wall forming a perimeter around the room. Let's calculate the amount of baseboards needed if the length of the baseboard is 2,5m. 

First let's calculate the perimeter of the room: 

(6,27 m + 4,37 m) x 2 =  21,28 rm 

rm - running meters, often used in construction. Equals 1m in SI units 

Now we can calculate the amount of baseboards needed: 

21,28 rm: 2,5 rm= 8,51 ≈ 9 pieces of baseboard

 

 

Geodesy and Geodetic Measurements

Geodesy is the science of measuring the size and shape of the Earth and the location of points on its surface. It includes land and construction surveying. 

The easiest or so called lower class geodesy is used for general construction (because of small distances). In road and land surveying the accuracy needs to be higher and the equipment used is a lot more complicated, because with longer distances the error margin also gets bigger (see example below). There we must install additional heights (temporary surveying staffs) to measure different sections and transfer their heights and angles. 

 

In this paragraph we well look closer into construction surveying, which is simple and only requires basic math. 

 

As we know water has the ability to always stay horizontal or as construction workers say it is horizontally levelled. In the old days water hoses with glass vials on both ends, that abled to see the water level, were used. 

Even nowadays this method is sometimes used (see picture below) but a lot of more tools have been developed since that are more exact in determining the level or plumb.   
 

 

A spirit is an instrument designed to indicate whether a surface is horizontal (level) or vertical (plumb).  

In the picture below is another example of a spirit, but instead of water  other liquids are used (usually alcohol such as ethanol) 

The bubble inside the spirit tube shows if the surface is level or not. If it’s centred between the lines on the tube, your object is level. If the bubble is to the right of the lines, your object slopes downward right-to-left. If the bubble is to the left of the lines, your object slopes downward left-to-right.

 

Now, if we need to level longer distances a tool called dumpy level (also builder's auto level)used. It is an optical instrument used to establish or check points in the same horizontal plane. The level instrument is set up on a tripod and set to a levelled condition using foot screws. The operator looks through the eyepiece of the telescope while an assistant holds a levelling rod vertical at the point under measurement.  

A better tool You can use is the laser level, which can be operated by only one person. It consists of a laser beam projector that can be affixed to a tripod, which is levelled according to the accuracy of the device and which projects a fixed red or green beam along the horizontal and/or vertical axis. 
 
 

 

The levelling rod, also called level staff, is used with a levelling instrument to determine the difference in height between points. The metric rod has major numbered graduations in meters and tenths of meters. When viewed through an instrument's telescope, the observer can easily visually interpolate a 1 cm mark to a quarter of its height, yielding a reading with accuracy of 2.5 mm.

 

Mean sea level 

In common usage, elevations are often cited in height above sea level.

MSL is a type of vertical datum – a standardised geodetic reference point – that is used as a chart datum in cartography.  Countries tend to choose the mean sea level at one specific point to be used as the standard „sea level” for all mapping and surveying in that country. However, zero elevation as defined by one country is not the same as zero elevation defined by another. In Estonia and in the Baltic sea region the MSL of Kronstadt is used. This was denoted by Mihhail von Reineke in 1840 after extensive measurings in the Baltic sea. Pictured below is the marking of MSL on the Obvodnõi canal bridge in Kronstadt.

 
 

 

Allikas: http://stengazeta.net/wp-content/uploads/10005290-siniy-most_.JPG 

 
Estonia is also planning on going over to the Amsterdam Ordnance Datum, which has the accuracy of  ± 0,2 mm per kilometre. 

In the field of construction a level is used to measure heights but when mapping larger areas a tachometer or precision GPS is used, as it enables you to measure not only height but also the angle.

Below a simple example of using a level.

 

Example

In this example, the geodesist has previously measured the foundation of an existing building to have a height 0.819 m above sea level. It will be used when we start marking down the planned foundation of the house with the height given in the project by the architect.

The zero point of the construction itself is the top surface of the first floor. All heights above it will be marked with a ( + ) sign and the ones below (such as a basement ) denoted by ( - ) sign. 

 

 
 

 

 

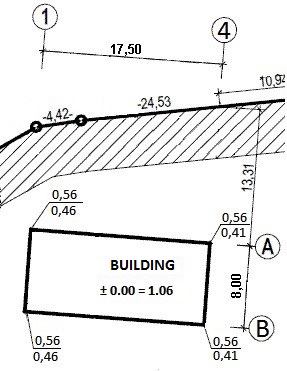
On the figure we see that the building has been designed with a height of 1.06 m above sea level (0 height is given by the surface of the first floor). The height of the ground is marked at the corners of the building. The upper 0.56 m tells us what altitude the ground around the building must remain, the number below indicates the current height of the ground in nature. 

Let’s do a small calculation:

1,06 – 0,56 = 0,50 m

This tells us that the ground must be 50 cm below the surface of the first floor.

 

Now we look what the level must show if we start to mark down the foundation of the building. Still looking at the figure above, we see that the horizontal beam of the level must have the height of 551 mm, meaning that from the sea level the horizontal beam must have the height:

819+ 551 = 1370 mm

But if we change the location of the level the result will also change. 

 

Next question that arises is how much should the starting point of the level be below the horizontal beam so it would correspond to the height of 1.06 m above sea level. 

We know, the horizontal beam is currently 1370 mm above sea level and we can do the following calculation: 

1370 – 1060 = 310mm  

 

 
 

 

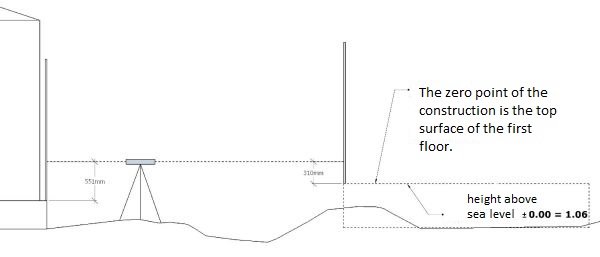
From the level we should be able to read out 0310, as shown in the figure above. Even though quite good laser tools exist, often construction workers still prefer to use optical measuring devices for longer distances as it is more exact since the laser beam will start to fade at larger distances.  

Mathematically we can look at this error as an occurring angle since the beam coming from the device is straight.

 

Calculating the error:

 

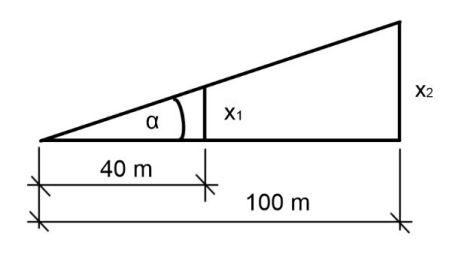
For example if we know the angle of the error we can use tangent to compare the values of x1 and x2 

 

Example 
If we want to show the error rate in mm we must first convert the length to get 40 000 mm. If we take the error to be only 0,1°, then  

x1 = tan 0,1° x 40 000 = 69,8 mm is already a very big difference, 

x2 = tan 0,1° x 100 000 = 174,5 mm, which is twice as big 

 

With a distance of 1 m and the same angle the error rate would only be 1,7 mm 

Therefor the surveyors must constantly correct the measurements in case of long distances, so a situation as pictured below would not happen. 

  
 
 

 

Source: unknown